|
George J. Friedman's Constraint Theory "CT is to Systems Engineering what Boolean Algebra is to Computer Design" |
What is Constraint Theory?
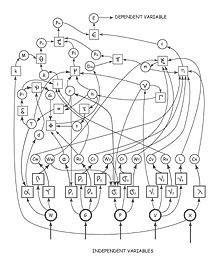
In a nutshell, Constraint Theory is a new branch of graph theory which can very quickly identify inconsistencies (overconstraint and underconstraint) in an engineering data model, make recommendations on how to fix it, and then will let you know whether a particular tradeoff analysis is an allowable computation. It is to systems engineering what Boolean Algebra is to computer design; it is a straightforward set of tools which will allow design teams to rapidly converge on an optimum set of variables without being hampered with the kinds of inconsistencies which routinely plague even the most straightforward of systems.
Unlike
the hundreds of design tools in the marketplace which attempt to
reconcile hundreds or thousands of design variables for rapid
convergence of a design, Constraint Theory will tell you before you
even begin if there are inherent problems with your math model which
these other tools cannot catch -- problems which, if undetected, can
waste tens of thousands of hours of effort down the line trying to
figure out why certain tradeoff and maximization attempts
consistently fail.
Proper application of Constraint Theory can greatly improve the utility of the model, leading the superior designs, design decision, and significantly faster model building for complex, multi-dimensional systems.
A Formal Introduction to Constraint Theory
Multidimensional math modeling is emerging as one of the most effective tools assisting the systems engineer in his efforts to manage the increasingly complexity of modern systems. In order to capture the necessary detail to develop realistic and trustworthy models, their dimensionality must encompass hundreds to thousands of variables, and the equations for the submodels are contributed by diverse technical and management teams.
Unfortunately, as the models grow in scope and complexity several problems arise. Often, some of the equations contributed by one technical team are in conflict with those from another team, rendering the total model inconsistent. Even more frequently, when computations are requested from this model, it is found that the set of dependent variable, independent variable and variables held constant do not permit an allowable computation.
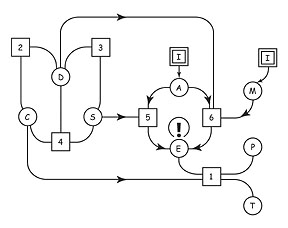Similarly,
when the managers who invested millions of dollars in the model
development request a greater variety of computations than those
originally envisioned, major problems in reprogramming and allowable
computational flow ensue. These issues are generally classed as
"well-posed" problems and are addressed by Constraint Theory, a
recent application of graph theory, specifically bipartite graphs.
(Note: Constraint Theory derives its name from Dr. Friedman's Ph.D. dissertation from 1967, entitled "Constraint Theory Applied to Mathematical Model Consistency and Computational Allowability". It is NOT about the "Theory of Constraints" recently popularized by Dr. Eliyahu Goldratt.)
Who will benefit from the use of Constraint Theory?
Aerospace and Defense Contractors, and others who must rapidly develop such complex systems, will benefit from this technology immediately.